年間、40冊前後、読書を楽しんでいるのですが、ほとんどの本で読後の満足感はあるものの、しばらく経つと全く内容を覚えていないことも多いということが悩みの種だったこともあって、手に取った本です。せっかく読書を楽しむなら、その質を高めたいですよね。
本書を読んで、納得するところが多かったのですが、特に、インプットした情報をアウトプットし、アウトプットすることで本から得た情報を知識とするということです。本書は、インプットからアウトプットへ繋げていくノウハウが詰まった本ですね。この過程を身につけ、有意義な読書ライフを楽しみたいと思います。
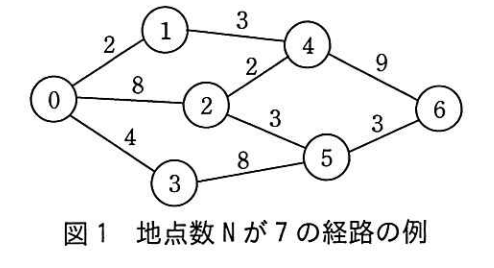
『アルゴリズムC〈第3巻〉グラフ・数理・トピックス』のp34で紹介されている「合併-発見アルゴリズム」をPythonで作ってみました。
「合併-発見アルゴリズム」は、以下のような用途で使われているようです。
配列dadの添え字で親子関係を表現している。例えば、dad[4]=>2なら、4の親が2となる。dad[2]=>-1なら要素2が集合の根(負数)を表す。要素xと要素yが同じ集合に属しているかを調べる場合は、xが属している集合の根の値とyが属している根の値を比較することで調べることができる。
class UnionFind: def __init__(self, n): self.dad = [-1 for _ in range(n)] def find(self, x, y, doit=False): i, j = x, y while self.dad[i] >= 0: i = self.dad[i] while self.dad[j] >= 0: j = self.dad[j] if doit and i != j: self.dad[j] = i return i == j
例えば、dad[8]=>4, dad[4]=>2, dad[2]=>-1のとき、8が属している集合の根は2となるが、3回配列を調べる必要がある。これをdad[8]=>2とすることで、探索回数を減らすことができる。
class UnionFind: def __init__(self, n): self.dad = [-1 for _ in range(n)] def find(self, x, y, doit=False): i, j = x, y while self.dad[i] >= 0: i = self.dad[i] while self.dad[j] >= 0: j = self.dad[j] # 道短縮法(path compression) while self.dad[x] >= 0: t = x x = self.dad[x] self.dad[t] = i while self.dad[y] >= 0: t = y y = self.dad[y] self.dad[t] = j if doit and i != j: self.dad[j] = i return i == j
(1),(2)の方法では、2つの集合を合併するとき、常にdad[j] = iとしていたが、根に重みを持たせることにより、子孫の数が多い方を根とする。
class UnionFind: def __init__(self, n): self.dad = [-1 for _ in range(n)] def find(self, x, y, doit=False): i, j = x, y while self.dad[i] >= 0: i = self.dad[i] while self.dad[j] >= 0: j = self.dad[j] # 道短縮法(path compression) while self.dad[x] >= 0: t = x x = self.dad[x] self.dad[t] = i while self.dad[y] >= 0: t = y y = self.dad[y] self.dad[t] = j # 重さ均衡法(weight balancing) if doit and i != j: if self.dad[j] < self.dad[i]: self.dad[j] += self.dad[i] - 1 self.dad[i] = j else: self.dad[i] += self.dad[j] - 1 self.dad[j] = i return i == j
(1)〜(3)について、以下を実行してみます。
if __name__ == "__main__": import pprint uf = UnionFind(10) # 0, 2, 4を同じグループ(A)に所属させる。 uf.find(0, 2, True) pprint.pprint(uf.dad) uf.find(0, 4, True) pprint.pprint(uf.dad) # 6, 8を同じグループ(B)に所属させる。 uf.find(6, 8, True) pprint.pprint(uf.dad) # 1, 3, 5, 7, 9を同じグループ(C)に所属させる。奇数グループ for i in range(3, 10, 2): uf.find(i - 2, i, True) pprint.pprint(uf.dad) uf.find(0, 8, True) # (A)と(B)を統合する。偶数グループ pprint.pprint(uf.find(0, 8)) pprint.pprint(uf.dad) pprint.pprint(uf.find(1, 8)) pprint.pprint(uf.dad) uf.find(1, 8, True) # 偶奇統合。自然数グループへ pprint.pprint(uf.find(1, 8)) pprint.pprint(uf.dad)
[-1, -1, 0, -1, -1, -1, -1, -1, -1, -1] # 0,2が同じグループへ
[-1, -1, 0, -1, 0, -1, -1, -1, -1, -1] # 0,2,4が同じグループへ
[-1, -1, 0, -1, 0, -1, -1, -1, 6, -1] # 6,8が同じグループへ
[-1, -1, 0, 1, 0, -1, -1, -1, 6, -1] # 1,3,5,7,9が同じグループへ
[-1, -1, 0, 1, 0, 1, -1, -1, 6, -1]
[-1, -1, 0, 1, 0, 1, -1, 1, 6, -1]
[-1, -1, 0, 1, 0, 1, -1, 1, 6, 1] # {0,2,4}, {6,8}, {1,3,5,7,9}の3グループ
True # {0,2,4}+{6,8}後、0,8は同じグループか?
[-1, -1, 0, 1, 0, 1, 0, 1, 6, 1]
False # 1,8は同じグループか?
[-1, -1, 0, 1, 0, 1, 0, 1, 6, 1]
True # 偶奇統合後、1,8は同じグループか?
[1, -1, 0, 1, 0, 1, 0, 1, 6, 1] # 8の親は6,6の親は1 (8→6→1)
[-1, -1, 0, -1, -1, -1, -1, -1, -1, -1] [-1, -1, 0, -1, 0, -1, -1, -1, -1, -1] [-1, -1, 0, -1, 0, -1, -1, -1, 6, -1] [-1, -1, 0, 1, 0, -1, -1, -1, 6, -1] [-1, -1, 0, 1, 0, 1, -1, -1, 6, -1] [-1, -1, 0, 1, 0, 1, -1, 1, 6, -1] [-1, -1, 0, 1, 0, 1, -1, 1, 6, 1] True [-1, -1, 0, 1, 0, 1, 0, 1, 0, 1] False [-1, -1, 0, 1, 0, 1, 0, 1, 0, 1] True [1, -1, 0, 1, 0, 1, 0, 1, 1, 1] # 8の親は1(8→1) 短縮されている!
[-3, -1, 0, -1, -1, -1, -1, -1, -1, -1] [-5, -1, 0, -1, 0, -1, -1, -1, -1, -1] [-5, -1, 0, -1, 0, -1, -3, -1, 6, -1] [-5, -3, 0, 1, 0, -1, -3, -1, 6, -1] [-5, -5, 0, 1, 0, 1, -3, -1, 6, -1] [-5, -7, 0, 1, 0, 1, -3, 1, 6, -1] [-5, -9, 0, 1, 0, 1, -3, 1, 6, 1] True [-9, -9, 0, 1, 0, 1, 0, 1, 0, 1] False [-9, -9, 0, 1, 0, 1, 0, 1, 0, 1] True [1, -19, 0, 1, 0, 1, 0, 1, 1, 1] # 根(値が負)に重みを持たせている。
データの数を100000として実行速度を調べてみました。
import random import time import union_find1 import union_find2 import union_find3 N = 10**5 print("#### (1)ナイーブな方法") uf = union_find1.UnionFind(N) start = time.perf_counter() for i in range(N): x = random.randint(0, N - 1) y = random.randint(0, N - 1) uf.find(x, y, True) print(time.perf_counter() - start) print("#### (2)道短縮法(path compression)") uf = union_find2.UnionFind(N) start = time.perf_counter() for i in range(N): x = random.randint(0, N - 1) y = random.randint(0, N - 1) uf.find(x, y, True) print(time.perf_counter() - start) print("#### (3)道短縮法(path compression) + 重さ均衡法(weight balancing)") uf = union_find3.UnionFind(N) start = time.perf_counter() for i in range(N): x = random.randint(0, N - 1) y = random.randint(0, N - 1) uf.find(x, y, True) print(time.perf_counter() - start)
(2)と(3)には顕著な速度差が見られませんでしたが、(1)の遅さは際立っていました。
#### (1)ナイーブな方法 18.461921999999998 #### (2)道短縮法(path compression) 0.2709850830000029 #### (3)道短縮法(path compression) + 重さ均衡法(weight balancing) 0.2369107500000034
作成したUnionFindを使って以下の問題を解いてみました。
昨年末に『スパコン富岳の挑戦 GAFAなき日本の戦い方』を読んだのですが、その中で岩田聡さんとのエピソードの紹介もありました。まさかTSUBAMEや富岳開発の先頭を走られた松岡聡さんとゲーム分野で活躍された岩田さんに接点があったなんて驚きでした。
今までゲームにのめり込んだこともほとんどないので、本の中で出てくるゲームについては名前を聞いたことがある程度の理解なのですが、岩田聡さんという方の魅力には十分触れられたような気がします。
わたしが見つけた「天才の定義」があります。
「人が嫌がるかもしれないことや、
人が疲れて続けられないようなことを、延々と続けられる人」、
それが「天才」だとわたしは思うんです。
公式ホームページ「第99回東京箱根間往復大学駅伝競走」のチームエントリー(PDF)から集計した各大学の上位10人の平均タイムに箱根駅伝の順位を並べてみました。
| 順位 | 大学 | 上位10人の平均タイム | 箱根駅伝順位 |
|---|---|---|---|
| 1 | 駒澤大学 | 28:24.91 | 1 |
| 2 | 青山学院大学 | 28:25.11 | 3 |
| 3 | 創価大学 | 28:25.21 | 8 |
| 4 | 中央大学 | 28:27.66 | 2 |
| 5 | 明治大学 | 28:39.05 | 12 |
| 6 | 東京国際大学 | 28:39.51 | 11 |
| 7 | 順天堂大学 | 28:40.34 | 5 |
| 8 | 東海大学 | 28:42.71 | 15 |
| 9 | 國學院大學 | 28:43.70 | 4 |
| 10 | 大東文化大学 | 28:45.04 | 16 |
| 11 | 山梨学院大学 | 28:49.41 | 14 |
| 12 | 東洋大学 | 28:49.93 | 10 |
| 13 | 日本体育大学 | 28:51.58 | 17 |
| 14 | 法政大学 | 28:52.19 | 7 |
| 15 | 早稲田大学 | 28:56.08 | 6 |
| 16 | 城西大学 | 28:56.59 | 9 |
| 17 | 立教大学 | 29:00.72 | 18 |
| 18 | 帝京大学 | 29:09.91 | 13 |
| 19 | 専修大学 | 29:12.04 | 20 |
| 20 | 国士舘大学 | 29:14.38 | 19 |
| 順位 | 大学 | 上位10人の平均タイム | 箱根駅伝順位 |
|---|---|---|---|
| 1 | 駒澤大学 | 1:02:13 | 1 |
| 2 | 國學院大學 | 1:02:21 | 4 |
| 3 | 順天堂大学 | 1:02:25 | 5 |
| 4 | 青山学院大学 | 1:02:57 | 3 |
| 5 | 山梨学院大学 | 1:02:59 | 14 |
| 6 | 中央大学 | 1:03:00 | 2 |
| 7 | 帝京大学 | 1:03:12 | 13 |
| 8 | 明治大学 | 1:03:12 | 12 |
| 9 | 法政大学 | 1:03:19 | 7 |
| 10 | 創価大学 | 1:03:20 | 8 |
| 11 | 東洋大学 | 1:03:24 | 10 |
| 12 | 城西大学 | 1:03:30 | 9 |
| 13 | 東海大学 | 1:03:30 | 15 |
| 14 | 早稲田大学 | 1:03:33 | 6 |
| 15 | 大東文化大学 | 1:03:46 | 16 |
| 16 | 日本体育大学 | 1:03:56 | 17 |
| 17 | 国士舘大学 | 1:04:06 | 19 |
| 18 | 専修大学 | 1:04:11 | 20 |
| 19 | 東京国際大学 | 1:04:16 | 11 |
| 20 | 立教大学 | 1:04:19 | 18 |
10,000mの上位10人の平均タイムと箱根駅伝順位の相関係数は0.66、ハーフマラソンの上位10人の平均タイムと箱根駅伝順位の相関係数は0.76でした。 箱根駅伝の各区間の距離は20km以上であることから、やはりハーフマラソンとの関係が深そうですね。
「優先度付きキューにも使われる二分ヒープ構造をRubyで実装してみる - $shibayu36->blog;」という記事を見かけましたので、Heapクラスを使ってダイクストラ法に取り組んでみました。 題材は、以前も取り組んだ「平成29年度春季基本情報午後問8」です。
h29h_fe_pm8.rb地点0から地点6までの最短距離を求めています。
% ruby h29h_fe_pm8.rb
13
- 言語学バーリ・トゥード
- 時限病棟 (実業之日本社文庫)
- 日本国紀
- 屋上のテロリスト (光文社文庫)
- 黒猫の小夜曲（セレナーデ） 「死神」シリーズ (光文社文庫)
- Excel VBAのプログラミングのツボとコツがゼッタイにわかる本[第2版]
- 大学入試がわかる本――改革を議論するための基礎知識
- ルパンの星 ルパンの娘 (講談社文庫)
- ホームズの娘 ルパンの娘 (講談社文庫)
- ルパンの帰還 ルパンの娘 (講談社文庫)
- ルパンの娘 (講談社文庫)
- 荒木飛呂彦の漫画術【帯カラーイラスト付】 (集英社新書)
- 「齋藤孝の相手を伸ばす!教え力」
- ルパンの絆
- 「ココロ」の経済学 ──行動経済学から読み解く人間のふしぎ (ちくま新書)
- 硝子の塔の殺人
- 渋沢栄一 君は、何のために「働く」のか―――絶対に後悔しない働き方、幸せになる働き方 (三笠書房 電子書籍)
- 数学ガールの秘密ノート/図形の証明
- マーケティングとは「組織革命」である。
- 二人の嘘 (幻冬舎単行本)
- 優しい死神の飼い方 「死神」シリーズ (光文社文庫)
- ＬＩＦＥ ＳＨＩＦＴ２―１００年時代の行動戦略
- 頭のよさとは「説明力」だ (詩想社新書)
- 再会 (講談社文庫)
- マスカレード・ゲーム
- ムゲンのｉ ： 上
- ムゲンのｉ ： 下
- 帰ってきたＫ２ 池袋署刑事課 神崎・黒木
- Ｋ２ 池袋署刑事課 神崎・黒木 (講談社文庫)
- 生き方
- メモの魔力 The Magic of Memos (NewsPicks Book)
- ミス・パーフェクトがいく！ (幻冬舎単行本)
- フェイクフィクション (集英社文芸単行本)
- マインド・クァンチャ Ｔｈｅ Ｍｉｎｄ Ｑｕｅｎｃｈｅｒ ヴォイド・シェイパ (講談社ノベルス)
- フォグ・ハイダ Ｔｈｅ Ｆｏｇ Ｈｉｄｅｒ ヴォイド・シェイパ (講談社ノベルス)
- スカル・ブレーカ Ｔｈｅ Ｓｋｕｌｌ Ｂｒｅａｋｅｒ ヴォイド・シェイパ (講談社ノベルス)
- ブラッド・スクーパ Ｔｈｅ Ｂｌｏｏｄ Ｓｃｏｏｐｅｒ ヴォイド・シェイパ (講談社ノベルス)
- ヴォイド・シェイパ Ｔｈｅ Ｖｏｉｄ Ｓｈａｐｅｒ (講談社ノベルス)
- 沈黙のパレード
- Pythonエンジニア育成推進協会監修 Python実践レシピ
- 奔流の海 (文春e-book)
- ダー・天使 (集英社文庫)
- フラッタ・リンツ・ライフ Flutter into Life スカイ・クロラ (C★NOVELS BIBLIOTHEQUE)
- ダウン・ツ・ヘヴン Ｄｏｗｎ ｔｏ Ｈｅａｖｅｎ スカイ・クロラ (C★NOVELS BIBLIOTHEQUE)
- ナ・バ・テア Ｎｏｎｅ Ｂｕｔ Ａｉｒ スカイ・クロラ (C★NOVELS BIBLIOTHEQUE)
- スカイ・クロラ (C★NOVELS BIBLIOTHEQUE)
- 苦しかったときの話をしようか
- ２つの粒子で世界がわかる 量子力学から見た物質と力 (ブルーバックス)
- 冬の狩人 狩人シリーズ
- スカイ・イクリプス Sky Eclipse スカイ・クロラ (C★NOVELS BIBLIOTHEQUE)
- クレィドゥ・ザ・スカイ Cradle the Sky スカイ・クロラ (C★NOVELS BIBLIOTHEQUE)
- 宇宙になぜ我々が存在するのか (ブルーバックス)
- 正義の天秤 (角川文庫)
- アキラとあきら 上 (集英社文庫)
- アキラとあきら 下 (集英社文庫)
- 先祖探偵
- クジラアタマの王様（新潮文庫）
- グッバイ・ヒーロー (講談社文庫)
- 木曜日にはココアを (宝島社文庫)
- お探し物は図書室まで
- ハヤブサ消防団 (集英社文芸単行本)
- 数学ガールの物理ノート/波の重ね合わせ
- 正義の天秤 アイギスの盾 (角川文庫)
- 雨に消えた向日葵 (幻冬舎文庫)
- サリエルの命題 (講談社文庫)
- ただいま神様当番
- 月曜日の抹茶カフェ
- 赤と青とエスキース
- シーソーモンスター (中公文庫)
- 忘れる読書 (PHP新書)
- 競争の番人 内偵の王子
- Google Apps Script目的別リファレンス 実践サンプルコード付き 第2版
- 競争の番人
- 天才たちの未来予測図（マガジンハウス新書）
- スパコン富岳の挑戦 GAFAなき日本の戦い方 (文春新書)
- 十字架のカルテ (文春文庫)
- 月の立つ林で
2022年は77冊、本を読みました。
get_book_titles.rb集計には以下のスクリプトを使用しています。
$ ruby get_book_titles.rb 2022
